LOS

  追踪控制算法中的视线法（Pure Pursuit Algorithm） 是一种常用于无人车、自主机器人或自动驾驶系统的路径跟踪算法。它的核心思想是通过确定一个“目标点”，使车辆以特定的转向角调整其行驶方向，从而逐步靠近预定路径。

视线法的基本原理

1. 视线点：
   • 视线点是路径上一个期望的参考点，航向调整是基于该点的相对位置。通常，视线点位于当前位置前方的某个固定或动态计算的距离处。
   • 从当前位置沿着路径找到一个距离为“前视距离”（Lookahead Distance）的目标点。
   • 如果当前并不在规划的路径上，则计算当前位置在路径上的垂直投影点（如果投影点存在）。从该投影点沿路径方向距离为“前视距离”的目标点。
2. 前视距离
   • 是从当前位置（或投影点）到视线点的距离。
   • 前视距离的选取直接影响路径跟踪的性能：
     • 较小的前视距离：能够紧密跟随路径，但可能会有较大的横向偏差或高频振荡。
     • 较大的前视距离：路径跟踪更平滑，但转向可能较迟缓，导致较大的路径误差。

3. 横向误差
   当前位置不在规划的路径上时，当前的位置到参考路径的垂直距离为横向误差

4. 视线角
   视线角是AUV当前位置到视线点连线与惯性坐标系（或北向）正方向之间的夹角。

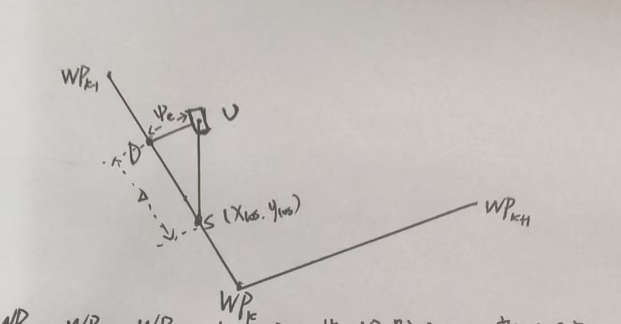
  如图所示，设路径由一系列路径点（Waypoints）$\mathrm{WP}{k-1}$, $\mathrm{WP}_k$, $\mathrm{WP}{k+1}$, $\dots$ 构成，车辆当前位于位置点 $U$，其在惯性坐标系中的位置为 $(x, y)$。将车辆在路径上的投影点记为 $D$，其坐标为 $(xd, y_d)$。从投影点 $D$ 向路径方向前进一个前视距离 $L_d$，可获得视线点 $(x{los}, y_{los})$，用于引导控制。
（1）横向误差（Lateral Error）
车辆当前位置 $(x, y)$ 与其在路径上的垂足 $(x_d, y_d)$ 之间的距离定义为横向误差 $y_e$，其计算公式为：

$$y_e = \sqrt{(x - x_d)^2 + (y - y_d)^2}$$

（2）视线角（Line-of-Sight Angle, LOS Angle）
视线角 $\psi{LOS}$ 是从当前位置 $(x, y)$ 指向视线点 $(x{los}, y_{los})$ 的方向角，可表示为：

$$\psi_{LOS} = \arctan2(y_{los} - y,\ x_{los} - x)$$