模糊（Fuzzy）控制算法

一、概念

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法，它是从行为上模仿人的模糊推理和决策过程的一种智能控制算法。模糊控制首先将操作人员或专家经验编成模糊规则，然后将来自传感器的实时信号模糊化，将模糊化后的信号作为模糊规则的输入，完成模糊推理，将推理后得到的输出量加到执行器上。

二、控制过程

所谓模糊控制，一般是用模糊的概念来描述偏差，并通过模糊推测得到模糊的给定量。比如，对偏差的描述常用“正大”，“正小”，“零”，“负小”，“负大”等模糊概念。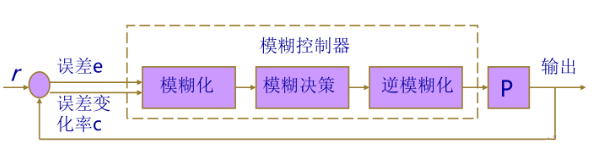

• 精确的测量值经过输入模糊化过程变成模糊集；
• 利用控制规则进行推理，即模糊决策，得到控制作用的模糊集；
• 将控制作用的模糊集按照一定的规则转化成精确值，此为逆模糊化。

三、前置基础知识

1. 模糊逻辑与传统逻辑的区别

模糊逻辑是模糊控制的重要工具，它与传统逻辑的主要区别在于变量的真值。

• 传统逻辑：
  真值只能是 0 或 1（非黑即白）。

  • 例：今天是否下雨？要么“是”，要么“否”。

• 模糊逻辑：
  真值可以是 [0, 1] 之间的任意值，表示某事的模糊程度。

  • 例：今天是“有点下雨”（隶属度为 0.6）。

2. 集合的基本概念

集合是数学中最基本的概念之一。传统集合的特点是清晰性，即一个元素要么属于该集合，要么不属于该集合。

例如：

• 集合 $A = {x \in \mathbb{R} | x > 0}$ 表示所有大于零的实数。
• 集合 $B = {1, 2, 3, 4}$ 表示四个具体的数字。

3. 域的基本概念

域是变量的取值范围，是模糊集合的定义基础。它通常由一个连续或离散的数值范围构成。

• 基本论域：
  基本论域是指变量的所有可能取值范围。在模糊控制中，每个输入或输出变量都有一个对应的基本论域。它定义了模糊集合的作用范围。
  示例:
  • 如果一个模糊控制系统的输入是温度，温度可能在 $[0, 100]$ ℃ 之间变化，那么温度的基本论域就是 $[0, 100]$。
  • 输出变量是风扇的转速，其基本论域可能是 $[0, 3000]$ rpm。

• 子论域:
  子论域是从基本论域中划分出来的一个子集，通常与特定的模糊集（如“低”、“中”、“高”等）相关联，用于描述变量的模糊值。
  示例:

  • 对于温度的基本论域 $[0, 100]$，可以定义以下子论域：
    • “低温”对应 $[0, 30]$。
    • “中温”对应 $[20, 70]$。
    • “高温”对应 $[60, 100]$。
  • 子论域之间通常有交叠，以符合模糊集合的特性。

• 基本论域$[a,b]$到子论域$[-n,n]$的转换关系：

  $$y=(x-\frac{a+b}{2})\frac{2n}{b-a}$$

4. 模糊集合

4.1. 数学定义

模糊集合 $A$ 定义在一个论域 $X$ 上，它是所有元素 $x \in X$ 与其隶属度 $\mu_A(x)$ 的集合：
[
A = {(x, \mu_A(x)) | x \in X, \mu_A(x) \in [0, 1]}
]
其中：

• $X$ 是论域（所有可能的元素集合），比如一个变量的取值范围；
• $\mu_A(x)$ 是隶属函数，表示元素 $x$ 属于模糊集合 $A$ 的程度；
• $\mu_A(x) \in [0, 1]$，即隶属度在 0 和 1 之间。

4.2. 模糊集合与传统集合的区别

1. 传统集合
在传统集合中，元素要么属于集合，要么不属于集合：

• 如果元素 $x$ 属于集合 $A$，则 $x \in A$，隶属度 $\mu_A(x) = 1$；
• 如果 $x$ 不属于集合 $A$，则 $\mu_A(x) = 0$。

例如：

• 定义集合 $A = {x | x \geq 18}$，表示成年人；
  • 如果 $x = 20$，则 $\mu_A(20) = 1$；
  • 如果 $x = 15$，则 $\mu_A(15) = 0$。

2. 模糊集合
模糊集合允许元素部分属于集合，属于的程度由隶属函数 $\mu_A(x)$ 表示。例如，“接近年轻的人”：

• 如果 $x = 20$ 岁，$\mu_A(20) = 1$（完全年轻）；
• 如果 $x = 30$ 岁，$\mu_A(30) = 0.5$（部分年轻）；
• 如果 $x = 50$ 岁，$\mu_A(50) = 0$（完全不年轻）。

5. 隶属度

隶属度（Membership Degree）是模糊集合理论中的核心概念，用来描述某个元素属于某模糊集合的程度。隶属度的值是一个介于 0 和 1 之间的实数，通过 隶属函数 来定义。

5.1. 隶属度的定义

隶属度通常用符号 $\mu_A(x)$ 表示，定义如下：

$$\mu_A(x) \in [0, 1]$$

其中：

• $x$ 是集合的元素；
• $\mu_A(x)$ 是 $x$ 属于模糊集合 $A$ 的隶属度。

隶属度具有以下特点：

• $\mu_A(x) = 1$ 表示 $x$ 完全属于集合 $A$；
• $\mu_A(x) = 0$ 表示 $x$ 完全不属于集合 $A$；
• $\mu_A(x) \in (0, 1)$ 表示 $x$ 部分属于集合 $A$，属于的程度由隶属度值表示。

5.2. 隶属函数

隶属函数是定义隶属度的数学表达式，决定了模糊集合的形状和性质。不同的隶属函数适用于不同的应用场景。

常见的隶属函数类型包括：

(1) 三角隶属函数
三角隶属函数是一种简单且常用的形式，定义为：

$$\mu_A(x) = \begin{cases} 0, & x \leq a \text{ 或 } x \geq c \\ \frac{x-a}{b-a}, & a \leq x \leq b \\ \frac{c-x}{c-b}, & b \leq x \leq c \end{cases}$$

• $a$ 和 $c$ 是底边的左右端点；
• $b$ 是顶点（隶属度为 1）。

示例：
模糊集合“中等温度”定义为：

• 当温度 $T$ 为 20℃时，$\mu_A(20) = 0$；
• 当温度 $T$ 为 50℃时，$\mu_A(50) = 1$；
• 当温度 $T$ 为 80℃时，$\mu_A(80) = 0$。

(2) 梯形隶属函数
梯形隶属函数是三角隶属函数的扩展，定义为：

$$\mu_A(x) = \begin{cases} 0, & x \leq a \text{ 或 } x \geq d \\ \frac{x-a}{b-a}, & a \leq x \leq b \\ 1, & b \leq x \leq c \\ \frac{d-x}{d-c}, & c \leq x \leq d \end{cases}$$

• $[a, b]$ 是上升部分；
• $[c, d]$ 是下降部分；
• $[b, c]$ 是平台部分，隶属度为 1。

(3) 高斯隶属函数
高斯隶属函数（Gaussian Membership Function）定义为：

$$\mu_A(x) = e^{-\frac{(x-c)^2}{2\sigma^2}}$$

• $c$ 是高斯曲线的中心；
• $\sigma$ 是曲线的宽度。

这种函数平滑连续，适合处理对边界敏感的问题。

(4) S型隶属函数
S型隶属函数用于描述平滑的上升趋势，定义为：

$$\mu_A(x) = \begin{cases} 0, & x \leq a \\ 2\left(\frac{x-a}{b-a}\right)^2, & a \leq x \leq \frac{a+b}{2} \\ 1 - 2\left(\frac{b-x}{b-a}\right)^2, & \frac{a+b}{2} \leq x \leq b \\ 1, & x \geq b \end{cases}$$

6. 模糊集合运算

模糊集合的基本运算包括交集、并集和补集，与传统集合类似，但使用的是隶属度进行操作：

• 交集（AND）：

  $$\mu_{A \cap B}(x) = \min(\mu_A(x), \mu_B(x))$$

• 并集（OR）：

  $$\mu_{A \cup B}(x) = \max(\mu_A(x), \mu_B(x))$$

• 补集（NOT）：

  $$\mu_{\neg A}(x) = 1 - \mu_A(x)$$

四、控制过程理解

例子：智能风扇速度控制

目标：设计一个模糊控制系统，根据环境温度调整风扇速度，保持室内舒适温度。

• 目标温度：$T_\text{target} = 25^\circ C$。

• 温度偏差：温度偏差的定义为：

  $$e = T_\text{current} - T_\text{target}$$

  其中：

  • $e > 0$ 表示室温高于目标温度，需要增加风扇速度；
  • $e < 0$ 表示室温低于目标温度，需要降低风扇速度。

• 风扇速度：转速的基本论域为 $[0, 1000]$（单位：RPM）。

1. 输入与输出的模糊集合

输入变量：温度偏差 $e$
偏差的基本论域为 $[-10, 10]$（单位：℃），划分为以下模糊集合：

• NB（负大）：$e \leq -5$
• NS（负小）：$-5 < e \leq -1$
• ZE（零）：$-1 < e < 1$
• PS（正小）：$1 \leq e < 5$
• PB（正大）：$e \geq 5$

输出变量：风扇速度调整 $\Delta V$
风扇速度的调整量的基本论域为 $[-300, 300]$（单位：RPM），划分为：

• NB（减速大）：$\Delta V \leq -200$
• NS（减速小）：$-200 < \Delta V \leq -50$
• ZE（不变）：$-50 < \Delta V < 50$
• PS（加速小）：$50 \leq \Delta V < 200$
• PB（加速大）：$\Delta V \geq 200$

2. 模糊规则设计

模糊规则根据温度偏差 $e$ 生成风扇速度调整 $\Delta V$。示例如下：

$e$	$\Delta V$（调整规则）
NB	PB（加速大）
NS	PS（加速小）
ZE	ZE（保持不变）
PS	NS（减速小）
PB	NB（减速大）

• 解释：
  • 如果偏差 $e$ 很负（NB），说明当前温度远低于目标温度，需要大幅度增加风扇速度；
  • 如果偏差 $e$ 很正（PB），说明当前温度远高于目标温度，需要大幅度减小风扇速度。

3. 隶属关系计算

隶属度函数
1. 输入变量：温度偏差 $ e $
基本论域：$[-10, 10]$
模糊集合及隶属度函数如下：
| 模糊集合 | 隶属度函数 |
| ——————— | ———————————————————————————————————————————————————————————— |
| NB（负大） | $\mu\text{NB}(e) = \begin{cases} 1 & e \leq -5 \ \frac{-1}{5}(e + 5) & -5 < e \leq -1 \ 0 & e > -1 \end{cases}$ |
| NS（负小） | $\mu\text{NS}(e) = \begin{cases} 0 & e \leq -5 \text{ 或 } e > -1 \ \frac{1}{4}(e + 5) & -5 < e \leq -1 \end{cases}$ |
| ZE（零） | $\mu\text{ZE}(e) = \begin{cases} 0 & e \geq 1 或e \leq -1 \ 1 - e & -1 < e < 1 \end{cases}$ |
| PS（正小） | $\mu\text{PS}(e) = \begin{cases} 0 & e \leq 1 \text{ 或 } e > 5 \ \frac{1}{4}(5 - e) & 1 < e \leq 5 \end{cases}$ |
| PB（正大） | $\mu_\text{PB}(e) = \begin{cases} 0 & e \leq 1 \ \frac{1}{5}(e - 1) & 1 < e \leq 5 \ 1 & e > 5 \end{cases}$ |

2. 输出变量：风扇速度调整 $\Delta V$
基本论域：$[-300, 300]$
模糊集合及隶属度函数如下：

模糊集合	隶属度函数
NB（减速大）	$\mu_\text{NB}(\Delta V) = \begin{cases} 1 & \Delta V \leq -200 \ \frac{-1}{100}(\Delta V + 200) & -200 < \Delta V \leq -100 \ 0 & \Delta V > -100 \end{cases}$
NS（减速小）	$\mu_\text{NS}(\Delta V) = \begin{cases} 0 & \Delta V \leq -200 \text{ 或 } \Delta V > -50 \ \frac{1}{150}(\Delta V + 200) & -200 < \Delta V \leq -50 \end{cases}$
ZE（不变）	$\mu_\text{ZE}(\Delta V) = \begin{cases} 0 &\Delta V \geq 50或 \Delta V \leq -50 \ 1 - \frac{ \Delta V }{50} & -50 < \Delta V < 50 \end{cases}$
PS（加速小）	$\mu_\text{PS}(\Delta V) = \begin{cases} 0 & \Delta V \leq 50 \text{ 或 } \Delta V > 200 \ \frac{1}{150}(\Delta V - 50) & 50 < \Delta V \leq 200 \end{cases}$
PB（加速大）	$\mu_\text{PB}(\Delta V) = \begin{cases} 0 & \Delta V \leq 200 \ \frac{1}{100}(\Delta V - 200) & 200 < \Delta V \leq 300 \ 1 & \Delta V > 300 \end{cases}$

隶属度表格

输入变量：温度偏差 $ e $

$ e $	$ \mu_\text{NB}(e) $	$ \mu_\text{NS}(e) $	$ \mu_\text{ZE}(e) $	$ \mu_\text{PS}(e) $	$ \mu_\text{PB}(e) $
-10	1	0	0	0	0
-5	1	0.0	0	0	0
-3	0.4	0.6	0	0	0
-1	0.0	1.0	0	0	0
0	0	0	1.0	0	0
1	0	0	0	1.0	0
3	0	0	0	0.6	0.4
5	0	0	0	0.0	1
10	0	0	0	0	1

输出变量：风扇速度调整 $\Delta V$

$\Delta V$	$\mu_\text{NB}(\Delta V)$	$\mu_\text{NS}(\Delta V)$	$\mu_\text{ZE}(\Delta V)$	$\mu_\text{PS}(\Delta V)$	$\mu_\text{PB}(\Delta V)$
-300	1	0	0	0	0
-200	1	0.0	0	0	0
-100	0.0	0.6667	0	0	0
0	0	0	1.0	0	0
100	0	0	0	0.6667	0
200	0	0	0	0.0	1
300	0	0	0	0	1

4. 计算

根据前面的分析和计算，我们已经得到输出变量的隶属度。现在我们需要从输出变量的隶属度推导出风扇的转速调整量。

步骤 1：确定输出变量的隶属度

输入误差 $ e = 3 $ 对应的隶属度值为：

• $ \mu_\text{NB} = 0 $
• $ \mu_\text{NS} = 0 $
• $ \mu_\text{ZE} = 0 $
• $ \mu_\text{PS} = 0.6 $
• $ \mu_\text{PB} = 0.4 $

根据模糊关系矩阵 $ R $，输出对应的隶属度值分别为：

• NB（减速大）：$ \mu_\text{NB} = 0.4 $
• NS（减速小）：$ \mu_\text{NS} = 0.6 $
• ZE（不变）：$ \mu_\text{ZE} = 0 $
• PS（加速小）：$ \mu_\text{PS} = 0 $
• PB（加速大）：$ \mu_\text{PB} = 0 $

步骤 2：去模糊化

我们可以使用质心法（Centroid Method）来进行去模糊化。质心法的公式为：

$$\Delta V = \frac{\sum \left( \mu_i \times V_i \right)}{\sum \mu_i}$$

其中：

• $ \mu_i $ 是对应模糊集合的隶属度值；
• $ V_i $ 是对应模糊集合的中心值。

输出变量的中心值

根据风扇转速调整量 $ \Delta V $ 的模糊集合定义，我们可以计算每个集合的中心值（即隶属度函数的“中点”）：

• NB（减速大）：$ V_{\text{NB}} = -250 $（大约为 -300 和 -200 之间的中心点）
• NS（减速小）：$ V_{\text{NS}} = -125 $（大约为 -200 和 -50 之间的中心点）
• ZE（不变）：$ V_{\text{ZE}} = 0 $（即没有调整）
• PS（加速小）：$ V_{\text{PS}} = 125 $（大约为 50 和 200 之间的中心点）
• PB（加速大）：$ V_{\text{PB}} = 250 $（大约为 200 和 300 之间的中心点）

质心法计算

$$\Delta V = \frac{(0.4 \times -250) + (0.6 \times -125) + (0 \times 0) + (0 \times 125) + (0 \times 250)}{0.4 + 0.6 + 0 + 0 + 0}$$ $$\Delta V = \frac{-100 - 75}{1}$$ $$\Delta V = -175$$

最终结果

根据去模糊化的计算，当前输入误差 $ e = 3 $ 对应的风扇速度调整量为 -175 RPM，即风扇应当减速。