一、什么是PID

PID 是比例-积分-微分控制（Proportional-Integral-Derivative Control）的缩写，是一种经典的控制算法，广泛应用于工业自动化中。它基于反馈控制原理，通过调整控制器的输出，确保被控对象的输出达到期望值（目标值）。

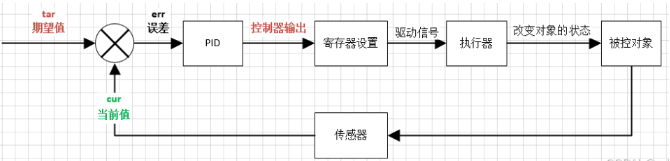
常用术语：

被控对象：需要控制的对象。
目标值：期望被控对象达到的状态量。
当前值：被控对象当前时刻的状态量。
反馈值：被控对象当前时刻的状态量。
输出量：控制器输出量，即PID的计算结果
误差：目标值-反馈值(当前值)
稳态误差：系统稳定状态下仍存在的误差。

1.1. PID的核心

PID控制由三个部分组成：

比例（P，Proportional）
- 根据当前误差大小进行控制，输出与误差成正比。
- 比例控制的作用是快速响应误差，但可能会导致稳态误差。
- 数学表达式：$Pout = Kp * e(t)$
  其中，$Kp$ 是比例增益，$e(t)$ 是当前误差。
积分（I，Integral）
- 考虑误差的累积，用于消除稳态误差。
- 如果误差长时间存在，积分项会逐渐增大，逼近目标值。
- s数学表达式：$Iout = Ki * \int e(t) dt$
  其中，$Ki$ 是积分增益，$\int e(t) dt$ 是误差的积分。
微分（D，Derivative）
- 根据误差的变化趋势进行控制，通过减缓误差的快速变化提高系统稳定性。
- 当误差快速变化时，微分控制部分会迅速反应，提供一个与变化率成比例的输出，减少可能的过冲或振荡。
- 数学表达式：$Dout = Kd * \frac{de(t)}{dt}$
  其中，$Kd$ 是微分增益，$\frac{de(t)}{dt}$ 是误差的微分。

1.2. PID控制器的输出

PID控制器的输出是比例、积分和微分三个部分的加权和，即：

$u(t) = Kp * e(t) + Ki * \int e(t) dt + Kd * \frac{de(t)}{dt}$

1.3. 常见的PID组合形式

P控制
- 从时域上看，只要存在偏差，比例就会立即对偏差进行控制，因此稳态时误差不一定为零
- 不足：比例控制只考虑当前误差，不考虑误差的变化趋势，可能导致系统不稳定。
- 适应于控制通道滞后较大、负荷变化较大、工艺参数允许有稳态误差的系统。
PI控制
- 从时域上看，只要存在偏差，积分就会不停对偏差积累，因此稳态时误差一定为零
- 不足：比例与积分动作都是对过去控制误差进行操作，不对未来控制误差进行预测，限制了控制性能。
- $PI$调节将比列调节的快速反应与积分调节消除静差的特点结合，实现好的调节效果。
- $PI$调节适用于控制通道滞后较小、负荷变化不大、工艺参数不允许有静差的系统。
PD控制
适用于舵机快速响应
对于惯性较大的对象，常常希望能加快控制速度，此时可增加微分作用。
- 比例控制对于惯性较大对象，控制过程缓慢，控制品质不佳。比例微分控制可提高控制速度，对惯性较大对象，可改善控制质量，减小偏差，缩短控制时间。
- 理想微分作用持续时间太短，执行器来不及响应。实际使用中，一般加以惯性延迟，称为实际微分。
- PD调节以比例调节为主，微分调节为辅，PD调节是有差调节。
- PD调节具有提高系统稳定性、抑制过渡过程最大动态偏差的作用。
- PD调节有利于提高系统响应速度。
- PD调节抗干扰能力差，一般只能应用于被调参数变化平稳的生产过程。
- 微分作用太强时，容易造成系统振荡。
PID控制
将比例、积分、微分三种调节规律结合在一起，只要三项作用的强度配合适当，既能快速调节，又能消除余差，可得到满意的控制效果。
- PID 控制作用中，比例作用是基础控制；微分作用是用于加快系统控制速度；积分作用是用于消除静差。
- 只要比例、积分、微分三种控制规律强度配合适当，既能快速调节，又能消除余差，可得到满意控制效果。
- $K_p$ 较小时，系统对微分和积分环节的引入较为敏感，积分会引起超调，微分可能会引起振荡，而振荡剧烈的时候超调也会增加。
- $K_p$ 增大时，积分环节由于滞后产生的超调逐渐减小，此时如果想要继续减少超调可以适当引入微分环节。继续增大 $K_p$ 系统可能会不太稳定，因此在增加 $K_p$ 的同时引入 $K_d$ 减小超调，可以保证在 $K_p$ 不是很大的情况下也能取得较好的稳态特性和动态性能。
- $K_p$ 较小时，积分环节不宜过大，$K_p$ 较大时积分环节也不宜过小（否则调节时间会非常地长），当使用分段PID ，在恰当的条件下分离积分，可以取得更好的控制效果。原因在于在稳态误差即将满足要求时，消除了系统的滞后。因此系统超调会明显减少。

1.4. PID优点和缺点

优点：

简单、易用，适合大多数线性系统。
实现成本低，计算开销小。

缺点：

参数$K_p、K_i、K_d$调整较复杂，需反复试验或借助算法优化。
对非线性系统或时变系统性能有限。

二、PID分类

PID控制器可以根据实现方式进行分类，主要分为模拟PID和数字PID。
简单的来讲，数字PID控制器是在模拟PID控制器的基础上，通过离散化的方法将其转化为适合数字计算的形式。在模拟PID控制器中，比例、积分、和微分操作都是连续信号处理，而数字PID控制器处理的是离散时间信号。离散化的核心是将连续时间的积分和微分运算转换成等效的离散时间算法。
我们在实际的工程应用中，通常使用离散的数字PID控制器，因为它具有更高的灵活性和更好的适应性。

三、模拟PID控制器

模拟PID控制器是通过电子元器件（如电阻、电容、运算放大器等）来实现比例、积分和微分控制的一种硬件形式。它的运行完全基于电路特性，因而具有即时性、简单性和可靠性的优点，尤其在数字控制尚未普及的年代应用广泛。

比例电路
比例控制直接将误差信号放大，比例系数$K_p$由电路增益决定。
- 实现：使用一个运算放大器和电阻网络调整增益
- 关键元件：电阻R和反馈网络决定$K_p$
积分电路
积分控制累积误差，用于消除稳态误差
- 实现：通过运算放大器的积分电路，典型配置为反馈网络中接一个电容C和电阻R。
- 关键元件：改变𝑅或𝐶的值调整积分时间常数。
微分电路
微分控制预测误差的变化趋势，用于加快系统响应。
- 实现：通过运算放大器的微分电路，输入端串联电容C，反馈接电阻R。
- 关键元件：改变𝑅或𝐶的值调整微分时间常数。
PID综合电路
将比例、积分、微分三个电路的输出信号通过
模拟PID控制器的输出公式为： $u(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{de(t)}{dt}$

四、数字PID控制器

数字式PID是用数字信号处理器（如微处理器、PLC）通过编程实现的PID控制算法。与传统模拟PID相比，数字式PID更加灵活，可以适应多种控制需求，并便于调试、优化和扩展。

数字式PID控制器的离散化形式有两种常见实现方式：位置型和增量型。

4.1. 位置型数字PID

位置型PID控制器直接计算输出$u(k)$,公式如下：

$u(k) = K_p e(k) + K_i \sum_{i=0}^{k} e(i) T+ K_d \frac{e(k) - e(k-1)}{T}$

其中:

$e(k)=r(k)-y(k)$:是当前时刻的误差，
$T$:是采样周期。
$K_p、K_i、K_d$:比例、积分、微分增益。

特点：

位置式PID是一种非递推式算法，可直接控制执行机构（如平衡小车），u(k)的值和执行机构的实际位置（如小车当前角度）是一一对应的，因此在执行机构不带积分部件的对象中可以很好应用。
控制输出基于误差的累计值计算，适用于需要精确位置控制的系统。
缺点：每次输出均与过去的状态有关，计算时要对e(k)进行累加，运算工作量大。